| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- console창
- Visual Studio Code
- run sql script
- github clone
- jupyter
- 단축키
- github token
- PHPStorm
- clone
- visualstudio code
- 파이썬
- 따옴표 삭제
- 오류
- error
- php
- 데이터베이스
- OrCAD 다운로드
- cmd
- Python
- 클론
- database
- csv
- 깃 토큰
- localhost
- 에러
- import data
- vscode
- error 해결
- DataGrip
- MySQL
- Today
- Total
개발 노트
5. 퀵 정렬(Quick Sort) 6.퀵 정렬(Quick Sort)의 구현 및 한계점 분석 본문
5. 퀵 정렬(Quick Sort) 6.퀵 정렬(Quick Sort)의 구현 및 한계점 분석
hayoung.dev 2024. 1. 30. 18:18- 굉장히 빠른 알고리즘.
- 분할 정복 알고리즘.
- 특정한 배열이 있을 때 나누어 계산.
- 평균 속도는 O(N * logN)
*logN은 상수에 가깝기 때문에 아주 작은 수이다. 예를 들어 2의 20제곱은 1000,000이므로 log2N에서 N이 1000,000일 때 log2N의 값은 20이다.
- 특정한 값을 긱준으로 큰 숫자와 작은 숫자를 나눈다. 배열을 두 집합으로 나눈다.
- 특정한 기준 값(피벗)을 설정하고 왼쪽과 오른쪽을 나눈다.
[정렬 예시]
1. 보통 가장 앞에 있는 값을 피벗 값으로 선택한다. -> 3이 피벗 값

2. 왼쪽에서 오른쪽으로 이동할 땐 피벗값보다 큰 값을 찾는다. -> 7
오른쪽에서 왼쪽으로 스캔할 땐 피벗값보다 작은 값을 찾는다. -> 2
그리고 그 둘을 바꾼다. -> 2와 7의 자리가 바뀜.

3. 이렇게 계속 반복하다가 -> 1과 8의 자리도 바뀜

그 다음 스켄한 큰값 8과 작은값 1이 교차해서 위치해있다면 그 작은값과 피벗값의 위치를 바꾼다. ->1과 3의 자리가 바뀜.
그리고 그 피벗값은 정렬이 된 것이다. -> 3의 위치 고정.

피벗값 3을 기준으로 왼쪽에 있는 숫자들은 3보다 작고, 오른쪽에 있는 숫자들은 3보다 큰 상태이다.
4. 두 집합으로 나누어 각각의 피벗값을 설정하고 똑같이 반복 수행한다. 이렇게 배열을 두 집합으로 나누는 것이 퀵 정렬이다.

이렇게 계속 두개로 분할을 해서 정렬하기 때문에 속도가 빠른 것이다.
[소스코드]
#include <stdio.h>
int number = 10; //총 데이터 개수
int data[10] = { 1, 10, 5, 8, 7, 6, 4, 3, 2, 9 };
void quickSort(int* data, int start, int end) {
//퀵 정렬 함수, start는 정렬을 수행하는 부분집합의 첫 번째 숫자, end는 마지막 숫자
if (start >= end) { //원소가 1개인 경우
return;
}
int key = start; //피벗값은 첫 번째 원소
int i = start + 1; //i는 왼쪽 출발 지점, 키값의 바로 오른쪽에 위치한 숫자이므로 +1
int j = end; //j는 오른쪽 출발 지점, 배열의 가장 마지막 숫자
int temp; //두 값을 바꾸기 위한 임시변수
while (i <= j) { //왼쪽에서 출발한 숫자와 오른쪽에서 출발한 숫자가 엇갈리면 멈춤
//i를 오른쪽으로 이동하며 data[key]보다 큰 값 고름
while (data[i] <= data[key]) {
i++;
}
//j를 왼쪽으로 이동하며 data[key]보다 작은 값 고름.
//단 j가 start보다 커서 start의 왼쪽으로 넘어가면 안되므로 조건 걸기
while (data[j] >= data[key] && j > start) {
j--;
}
if (i > j) { //엇갈린 상태라면 키 값과 교체
temp = data[j];
data[j] = data[key];
data[key] = temp;
}
else { //엇갈리지 않았다면 j와 i를 교체
temp = data[j];
data[j] = data[i];
data[i] = temp;
}
}
//다시 j를 기준으로 정렬되고 남은 j의 왼쪽과 j의 오른쪽을 퀵 정렬함
//재귀함수
quickSort(data, start, j - 1);
quickSort(data, j + 1, end);
}
int main(void) {
quickSort(data, 0, number - 1); //0부터 9까지 퀵 정렬 수행
//정렬 이후에 데이터 출력
for (int i = 0; i < number; i++) {
printf("%d ", data[i]);
}
}
출력 결과

하지만 최악의 경우에는 시간복잡도가 O(N*N)이다. 대부분 정렬되어 있는 경우가 해당된다.
예를들어 1 2 3 4 5 6 7 8 9 가 있을 때 피벗값보다 모든 값이 크기 때문에
1 2 3 4 5 6 7 8 9 10 과 같이 정렬된 피벗값이 항상 왼쪽에 위치하게 된다.
즉 정렬된 피벗값이 중간 정도에 위치해있어야 분할정복의 이점을 쓸 수 있는데 그렇지 못하고 10 + 9 + ... 의 횟수로 정렬을 하게 된다. 이렇게 이미 정렬이 되어있는 경우에는 굉장히 느리기 때문에 이런 경우에는 삽입정렬을 사용해야 빠르다.
즉 정렬할 데이터에 따라 그에 알맞는 알고리즘을 사용하여야 한다.
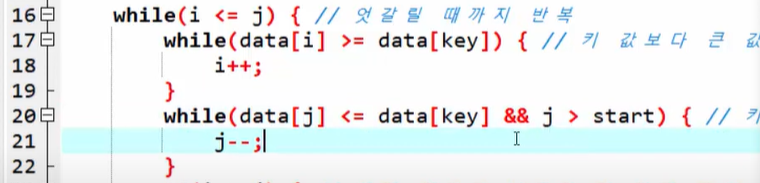
[내림차순으로 정렬하고 싶을 때]
기존 코드에서 사진처럼
17줄의 <를 >로,
20줄의 >를 <로 바꾼다.
출력 결과

'알고리즘 공부 : 24.01.18~ > 1. 알고리즘 기초 정렬' 카테고리의 다른 글
| 백준과 깃허브 연동 (0) | 2024.01.30 |
|---|---|
| 7. 기초 정렬 알고리즘 문제 풀이 (0) | 2024.01.30 |
| 4. 삽입 정렬(Insertion Sort) (0) | 2024.01.24 |
| 3. 버블 정렬(Bubble Sort) (1) | 2024.01.24 |
| 2. 선택 정렬(Selection Sort) (2) | 2024.01.24 |




